Please enter the code we just sent to whatsapp 91-11-46710500 to proceed
Didn't Receive OTP?
Mathematics contains patterns and rules that allow students to solve problems in simpler and more logic-based ways. One of these rules is the associative property, which is quite a simple and powerful idea that allows students to comprehend how numbers can associate with one another. Regardless of the operation you are studying (addition, multiplication) the associative property is a simple way to make math more straightforward, and potentially even fun!
In this blog post we are going to cover the definition of the associative property, provide some examples of associative property, and show how the associative property applies to both addition and multiplication. This will prove to be a valuable resource for kids, parents, and teachers; we all benefit from cultivating strong math foundations.
The associative property states that (the properties of) addition and multiplication can define how numbers are associated or grouped together without altering the end result.
In other words:
The result will not be affected by how we associate (or group) the numbers in addition or multiplication.
Formula:
(a + b) + c = a + (b + c)
This means that it doesn't matter which two numbers you add together first— the sum will always equal the same.
Formula:
(a × b) × c = a × (b × c)
Again, it doesn't matter how we group the numbers together; the product will always be the same.
Not Applicable To:
The Associative property does not apply to:
Subtraction
Division
Changing the grouping in these (or similar) operations will affect the outcome.
Associative Property Examples
To clarify this idea
let’s look at some examples:
Associative Property of Addition Example Example 1:
(3 + 4) + 5 = 7 + 5 = 12
3 + (4 + 5) = 3 + 9 = 12
Both the same outcome!
Associative Property of Multiplication Example Example 2:
(2 x 3) x 4 = 6 x 4 = 24
2 x (3 x 4) = 2 x 12 = 24
Again, the same result!
Non-Associative Operation Example Subtraction Example:
(10 - 5) - 2 = 5 - 2 = 3
10 - (5 - 2) = 10 - 3 = 7
Different results → Not associative!
When kids learn the math associative property, they can:
Solve problems quicker.
Better understand how numbers relate to each other.
Improve their mental math skills.
Create a solid base for Algebra and higher-level math.
Promote their confidence with equations and expressions.
Teaching Suggestions Kids almost always enjoy math more when it is visual, hands-on, and interactive.
Here are some simple ways to teach the associative property for kids:
Use Objects from Everyday Life
Use apples, building blocks or crayons, grouped into pairs of 3.
Allow the kids to regroup and count again. Point out that the total still stays the same.
Draw Brackets
Write numbers on a whiteboard.
Draw brackets around different pairs and solve as a group.
Make it a Game
"Group and solve" challenge: Give your child three numbers for them to solve two ways by grouping them in different ways to check for results.
Use Stories
"E.g. If Sarah eats 2 cookies, and then her brother gives her 3 more, and then her friend gives her 4 more... does it matter who initially gave them?
Stories can help Math become more relatable.
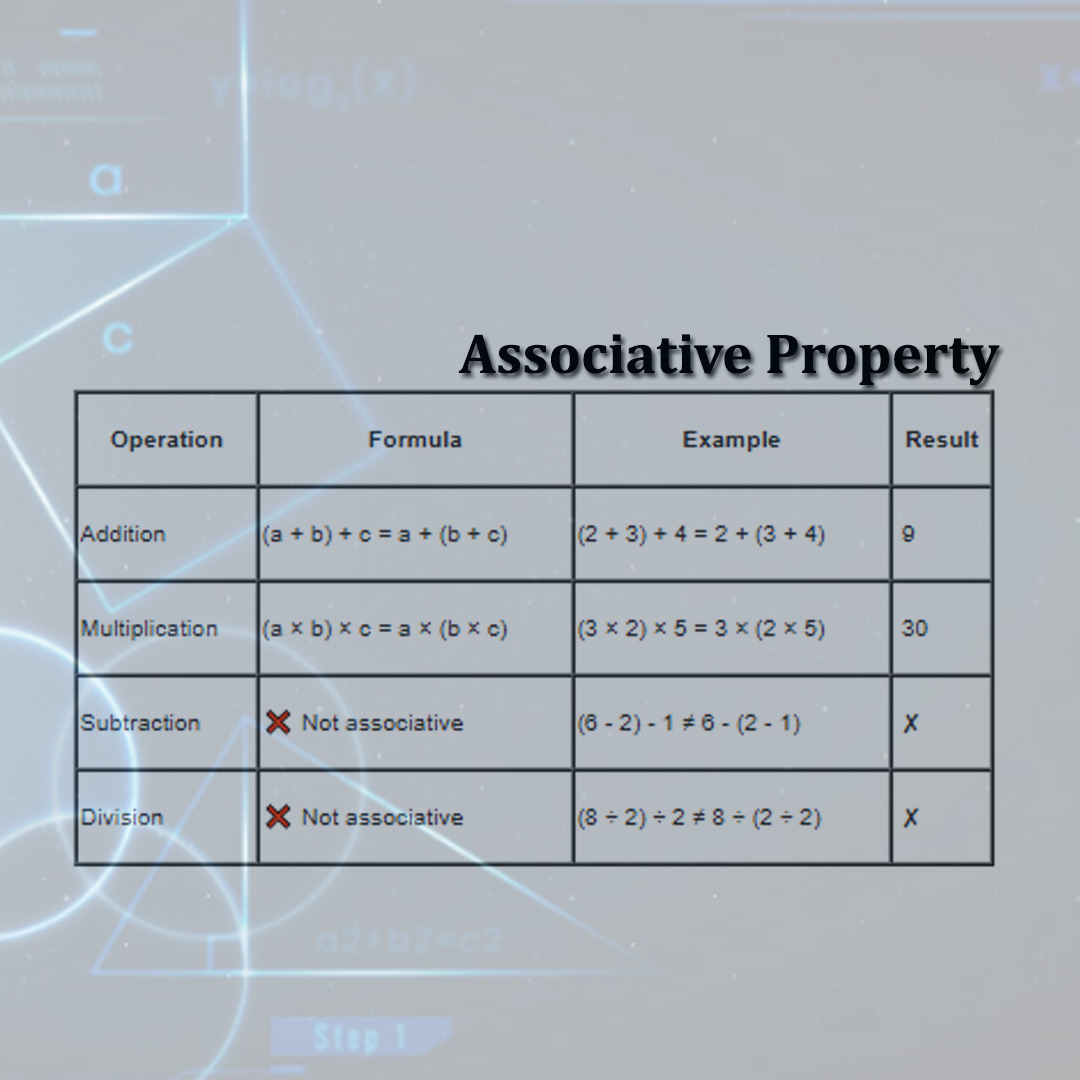
|
Operation |
Formula | Example |
Result |
|---|---|---|---|
|
Addition |
(a + b) + c = a + (b + c) | (2 + 3) + 4 = 2 + (3 + 4) |
9 |
|
Multiplication |
(a × b) × c = a × (b × c) | (3 × 2) × 5 = 3 × (2 × 5) |
30 |
|
Subtraction |
❌ Not associative | (6 - 2) - 1 ≠ 6 - (2 - 1) |
✘ |
|
Division |
❌ Not associative | (8 ÷ 2) ÷ 2 ≠ 8 ÷ (2 ÷ 2) |
✘ |
Fun Facts about the Associative Property
"Associative" is from the root word "associate" or grouping.
Associative property is one of the three basic properties of numbers (with commutative and distributive).
Once kids understand associative property, they can use it in algebra, coding, even robotics, to complete calculations more quickly.
Understanding associative property early will help kids later on when they are dealing with bigger math problems!
Q1. What's the main thing to remember about associative property?
That the grouping of numbers in addition or multiplication, does not change the result.
Q2. Does it work with four or more numbers?
Yes! As long as you're an acting solely on addition or multiplication, yes.
Q3. Is the associative property used in algebra?
Yes, it is very useful for simplifying algebraic expressions.
Q4. How is it different from commutative property?
Associative: changes grouping (it is ok to change parentheses)
Commutative: changes order
Experience Math with a Smile with Bambinos.Live Math Program
The associative property is just one of the many exciting math concepts that children will experience in the Bambinos.Live Math Program.
At Bambinos.live, we know that math is not about numbers, it’s about thinking!
Our fun, exciting online math classes help kids:
Understand foundational concepts such as associative, commutative, and distributive properties
Solve real-world problems
Build speed and accuracy
Foster an early love of math and learning
Learn via fun activities, puzzles, stories, and interactive games
Taught by certified, experienced teachers
Available for children aged 6–10
Don’t let your child miss out on mastering math in a fun way.
Alpha Math offers a game-based learning experience with a unique four-step approach to mastering every concept in math. Schedule a Free Class Now